AtCoder: ABC126

2020.08.26

A – Changing a Character

問題

問題へのリンク

解法

K文字目を小文字に変換して出力するだけ。

実装


#include<iostream>
#include<vector>
#include<map>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstdlib>

#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define REP(i,n)   FOR(i,0,n)
#define MOD 1000000007

using namespace std;

typedef long long int ll;

const ll INF=(ll)1e18;

int main(){
  int N,K;
  cin >> N >> K;

  string S;
  cin >> S;
  S[K-1] = tolower(S[K-1]);
  cout << S << endl;
}

B – YYMM or MMYY

問題

問題へのリンク

解法

YYには制約は無いが、MMについては01〜12という制約がある。よって、1〜2文字目と3〜4文字目について、01〜12かどうかをチェックすればよい。
・1〜2文字目と3〜4文字目が両方01〜12の場合：AMBIGUOUS
・1〜2文字目のみ01〜12の場合：MMYY
・3〜4文字目のみ01〜12の場合：YYMM
・1〜2文字目と3〜4文字目が両方01〜12以外の場合：NA

実装


#include <bits/stdc++.h>
using namespace std;

#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define REP(i,n)   FOR(i,0,n)
#define ALL(a)     (a).begin(),(a).end()
#define RALL(a)     (a).rbegin(),(a).rend()
#define PRINT(a)   cout << (a) << endl

#define pb push_back
#define eb emplace_back
#define mp make_pair
#define Fi first
#define Se second

#define debug(x) cerr << x << " " << "(L:" << __LINE__ << ")" << '\n';

using ll = long long int;
using P = pair<int,int>;
using vi = vector<int>;
using vvi = vector<vi>;
using vvvi = vector<vvi>;
using pii = pair<int, int>;

template <typename T> using PQ = priority_queue<T>;
template <typename T> using minPQ = priority_queue<T, vector<T>, greater<T>>;

template<class T>bool chmax(T &a, const T &b) { if (a<b) { a=b; return 1; } return 0; }
template<class T>bool chmin(T &a, const T &b) { if (b<a) { a=b; return 1; } return 0; }

const int INF = 1001001001;
const ll LINF = 1001001001001001001ll;
const int MOD = 1e9 + 7;

int main(){
  string S;
  cin >> S;
  // 1〜2文字目を数値に変換
  int x = (S[0]-'0')*10+(S[1]-'0');
  // 3〜4文字目を数値に変換
  int y = (S[2]-'0')*10+(S[3]-'0');

  if(1<=x && x<=12 && 1<=y && y<=12){
    cout << "AMBIGUOUS" << endl;
  }else if(1<=x && x<=12){
    cout << "MMYY" << endl;
  }else if(1<=y && y<=12){
    cout << "YYMM" << endl;
  }else{
    cout << "NA" << endl;
  }
}

C – Dice and Coin

問題

問題へのリンク

解法

1回目に出たサイコロの数をxとする。xがK以上ならそのまますぬけ君の勝ちになる。xがK未満の場合、xを倍々にしていってK以上になる回数をtとすると、連続してコインの表が出続ける確率は、(1/2)tとなる。
最初にサイコロの数xがでる確率は等しく1/nなので、各xごとに上記の確率を求めて1/nすればよい。

実装


#include <bits/stdc++.h>
using namespace std;

#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define REP(i,n)   FOR(i,0,n)
#define ALL(a)     (a).begin(),(a).end()
#define RALL(a)     (a).rbegin(),(a).rend()
#define PRINT(a)   cout << (a) << endl

#define pb push_back
#define eb emplace_back
#define mp make_pair
#define Fi first
#define Se second

#define debug(x) cerr << x << " " << "(L:" << __LINE__ << ")" << '\n';

using ll = long long int;
using P = pair<int,int>;
using vi = vector<int>;
using vvi = vector<vi>;
using vvvi = vector<vvi>;
using pii = pair<int, int>;

template <typename T> using PQ = priority_queue<T>;
template <typename T> using minPQ = priority_queue<T, vector<T>, greater<T>>;

template<class T>bool chmax(T &a, const T &b) { if (a<b) { a=b; return 1; } return 0; }
template<class T>bool chmin(T &a, const T &b) { if (b<a) { a=b; return 1; } return 0; }

const int INF = 1001001001;
const ll LINF = 1001001001001001001ll;
const int MOD = 1e9 + 7;

int main(){

  int N,K;
  cin >> N >> K;

  double ans = 0;

  FOR(i,1,N+1){
    int t = i;
    double s = 1.0/N;
    while(t < K){
      s *= 0.5;
      t = t << 1;
    }
    ans += s;
  }

  cout << setprecision(12) << ans << endl;
}

D – Even Relation

問題

問題へのリンク

解法

とある頂点（例えば頂点1）の色を決めて（例えば白）、そこから隣接する頂点への距離が偶数の場合は同じ色（白）、奇数の場合は違う色（黒）に塗っていけば良い。
実装方法は深さ優先探索や幅優先探索を使えばよい。（今回の実装例は幅優先探索とした）

実装


#include <bits/stdc++.h>
using namespace std;

#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define REP(i,n)   FOR(i,0,n)
#define ALL(a)     (a).begin(),(a).end()
#define RALL(a)     (a).rbegin(),(a).rend()
#define PRINT(a)   cout << (a) << endl

#define pb push_back
#define eb emplace_back
#define mp make_pair
#define Fi first
#define Se second

#define debug(x) cerr << x << " " << "(L:" << __LINE__ << ")" << '\n';

using ll = long long int;
using P = pair<int,int>;
using vi = vector<int>;
using vvi = vector<vi>;
using vvvi = vector<vvi>;
using pii = pair<int, int>;

template <typename T> using PQ = priority_queue<T>;
template <typename T> using minPQ = priority_queue<T, vector<T>, greater<T>>;

template<class T>bool chmax(T &a, const T &b) { if (a<b) { a=b; return 1; } return 0; }
template<class T>bool chmin(T &a, const T &b) { if (b<a) { a=b; return 1; } return 0; }

const int INF = 1001001001;
const ll LINF = 1001001001001001001ll;
const int MOD = 1e9 + 7;

int main(){
  int N;
  cin >> N;

  vector<vector<P>> edge(N);
  vi col(N,-1);

  REP(i,N-1){
    int u,v,w;
    cin >> u >> v >> w;
    u--; v--;
    edge[u].emplace_back(v,w);
    edge[v].emplace_back(u,w);
  }

  queue<int> q;
  col[0]=0;
  q.push(0);

  while(!q.empty()){
    int x = q.front();
    q.pop();
    
    for(auto e: edge[x]){
      int y = e.first;
      int w = e.second;
      if(col[y]!=-1)continue;

      if(w%2==0){
        col[y] = col[x];
      }else{
        col[y] = col[x] ^ 1;
      }
      q.push(y);
    }
  }

  REP(i,N){
    cout << col[i] << endl;
  }
}

E – 1 or 2

問題

問題へのリンク

解法

各X、Y、Zについて、総和が偶数ということは、Zが偶数の場合はXとYは同じ（両方とも1 or 両方とも2）、Zが奇数の場合はXとYは異なる（1と2の組み合わせ）となる。
ここで入力例2を例にカードをノード、Zを辺の重みとしてグラフ化してみる。すると、グラフの連結成分のうち、1つのノードの数字が決まれば、残りのノードの数字も決まることがわかる。（下図では数字を色で表している）
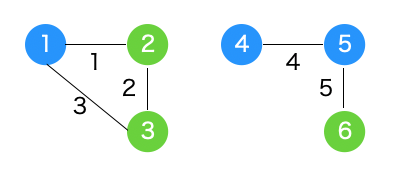
よって、連結成分ごとに1つのノードの色（つまり、1枚のカードの数字）がわかればよいということになる。よって連結成分の数が答えになる。
なお、連結成分の数はUnion Findを使えば求められる。

実装


#include <bits/stdc++.h>
using namespace std;

#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define REP(i,n)   FOR(i,0,n)
#define ALL(a)     (a).begin(),(a).end()
#define RALL(a)     (a).rbegin(),(a).rend()
#define PRINT(a)   cout << (a) << endl

#define pb push_back
#define eb emplace_back
#define mp make_pair
#define Fi first
#define Se second

#define debug(x) cerr << x << " " << "(L:" << __LINE__ << ")" << '\n';

using ll = long long int;
using P = pair<int,int>;
using vi = vector<int>;
using vvi = vector<vi>;
using vvvi = vector<vvi>;
using pii = pair<int, int>;

template <typename T> using PQ = priority_queue<T>;
template <typename T> using minPQ = priority_queue<T, vector<T>, greater<T>>;

template<class T>bool chmax(T &a, const T &b) { if (a<b) { a=b; return 1; } return 0; }
template<class T>bool chmin(T &a, const T &b) { if (b<a) { a=b; return 1; } return 0; }

const int INF = 1001001001;
const ll LINF = 1001001001001001001ll;
const int MOD = 1e9 + 7;

class UnionFindTree{
  public:
    vector<int> rank,p,count;

    UnionFindTree() {}

    UnionFindTree(int size){
      rank.assign(size, 0);
      p.assign(size, 0);
      count.assign(size,1);
      REP(i,size)makeSet(i);
    }

    void makeSet(int x){
      p[x] = x;
      rank[x] = 0;
    }

    bool same(int x, int y){
      return findSet(x) == findSet(y);
    }

    void unite(int x, int y){
      if(findSet(x) == findSet(y))return;

      x = findSet(x);
      y = findSet(y);
      
      if(rank[x] > rank[y]){
        p[y] = x;
      }else{
        p[x] = y;
        if(rank[x] == rank[y]){
          rank[y]++;
        }
      }

      int tmp = count[x] + count[y];
      count[x] = tmp;
      count[y] = tmp;
    }

    int findSet(int x){
      if(x != p[x]){
        p[x] = findSet(p[x]);
      }
      return p[x];
    }

    int getCount(int x){
      return count[findSet(x)];
    }

    void print(){
      REP(i,p.size()){
        cout << p[i] << " ";
      }
      cout << endl;
      REP(i,p.size()){
        cout << rank[i] << " ";
      }
      cout << endl;
    }

};

int main(){
  int n,m;
  cin >> n >> m;
  UnionFindTree tree(n);
  REP(i,m){
    int x,y,z;
    cin >> x >> y >> z;
    x--;y--;

    tree.unite(x,y);
  }

  set<int> st;
  REP(i,n){
    st.insert(tree.findSet(i));
  }
  cout << st.size() << endl;
}

コメント

タイトルとURLをコピーしました